【译】数据结构与算法——快速排序

发表于 2019-08-20 更新于 2020-12-04 分类于 Algorithm club

快速排序（Quicksort）是历史上最著名的算法之一。由 Tony Hoare 于 1959年发明，那是一个对递归概念尚且比较模糊的时代。

下面是一个 Swift 实现的简单版，较容易理解：

func quicksort<T: Comparable>(_ a: [T]) -> [T] {
  // 递归终止条件
  guard a.count > 1 else { return a }
  
  // 
  let pivot = a[a.count/2]
  let less = a.filter { $0 < pivot }
  let equal = a.filter { $0 == pivot }
  let greater = a.filter { $0 > pivot }

  return quicksort(less) + equal + quicksort(greater)
}

将如下测试代码放到 playground 中运行：

1 2	let list = [ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ] quicksort(list)

当给定一个数组，函数 quicksort() 首先通过变量 “pivots” 将它切分成三部分。这里，我们取数组的中间元素来作为“主元”（稍后会介绍其它取得主元的方法）。

关于“pivot”的翻译：打扑克斗地主时，如果一把连牌正好少中间那张牌，导致上下连不能一起出牌，被称为“缺轴”，这与本文中的 “pivot” 意思相同。在理解快速排序之后，也可以发现 “pivot” 越是接近数组的“中位数”越好，可见“pivot”被译为轴元才更贴切，也更容易被理解。但是《算法导论》这本最权威的著作没有采用，为了保持一致性，本文也采用了“主元”这个翻译。

所有小于主元的元素放到 “less” 数组中。所有等主元的放到 equal 数组中。如你所料，所有大于主元的都放入 greater 数组中。这就是为什么范型 T 必须遵循 Comparabel 协议，只有这样，才能对元素进行 <, ==, 以及 > 等比较操作。

一旦得到这三个数组，函数 quicksort() 就会对 less 数组以及 greater 数组进行递归排序，最终将排好序的子数组与 equal 数组合并，从而得到最终结果。

例子

下面通过例子来进行逐步讲解。初始数组如下：

[ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]

首先，我们选出主元 8。这是因为它正好位于数组的中间位置。接下来，我们将数组分成 less, equal, 和 greater 三个部分：

less:    [ 0, 3, 2, 1, 5, -1 ]
equal:   [ 8, 8 ]
greater: [ 10, 9, 14, 27, 26 ]

看来我们选择了一个不错的主元，刚好将原数组一切为二，使得 less 、 greater 包涵的元素数量相同。

注意此时 less 和 greater 都还是无序的。所以我们需要再次调用 quicksort()，以便对其进行排序。与之前操作相同，选出主元，将子数组继续切分成三个更小的数组。

这里我们仅以 less 数组为例进行说明：

[ 0, 3, 2, 1, 5, -1 ]

此次我们选择的主元元素是位于中间的 1（当然选择 2也可以，无关紧要）。再次通过主元创建三个子数组：

less:    [ 0, -1 ]
equal:   [ 1 ]
greater: [ 3, 2, 5 ]

还没完，继续对 less and greater 数组递归调用 quicksort()。继续对 less 进行说明：

[ 0, -1 ]

选择 -1作为主元。此时拆分后对子数组如下：

less:    [ ]
equal:   [ -1 ]
greater: [ 0 ]

因为已经没有比 -1 更小的数，所以less 数组为空；其它两个数组各包含一个数值。这意味着递归至此结束，我们可以继续对先前的 greater 进行排序了。

greater 数组如下：

[ 3, 2, 5 ]

与先前相同：挑选位于中间的元素 2 作为主元，并以此拆分为子数组：

less:    [ ]
equal:   [ 2 ]
greater: [ 3, 5 ]

注意，如果选择 3 作为主元，那么直接就可以结束了。但是现在不得不继续对 greater 进行递归操作，以保证它是排好序的。这也是为什么选择一个好的主元至关重要。一旦你选择很多“糟糕”的主元，那么快速排序将会变得很慢。 More on that below.

继续对 greater 拆分后发现：

less:    [ 3 ]
equal:   [ 5 ]
greater: [ ]

已经无法继续再分，递归至此已经结束。

这一处理过程会不断重复，直至所有的子数组都排好序。如下图：

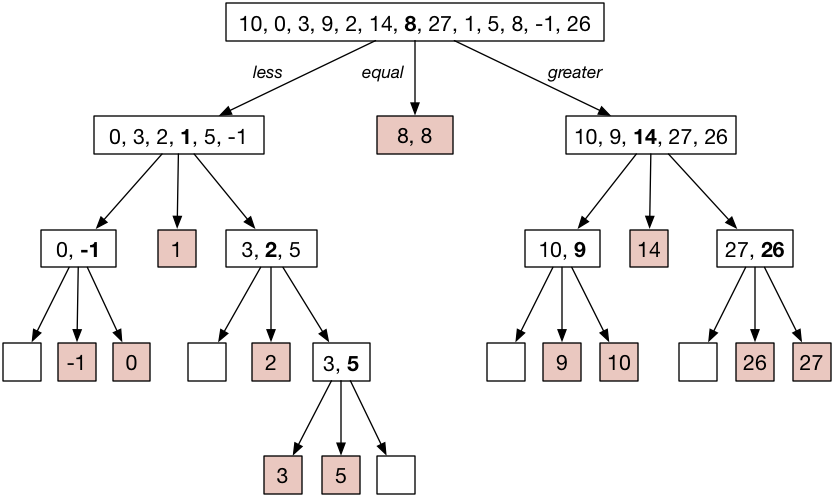
Example

注意到图中高亮的元素了吗，正是排好序的数组：

[ -1, 0, 1, 2, 3, 5, 8, 8, 9, 10, 14, 26, 27 ]

此图也表明了，8 是一个非常好的初始主元，因为它也正好位于排好序后数组的中间位置。

希望这能让你对快速排序的原理有一个大致的了解。但不幸的是，因为我们对同一个数组调用了三次 filter()，所以这个快速排序并不怎么快。还有更好的方式对数组进行拆分。

分治

围绕着主元对数组进行分割的操作被称为 分治（Partitioning），有几种不同方案：

例如有如下数组：

[ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]

我们选择位于正中的元素 8 作为主元，对数组进行分治：

[ 0, 3, 2, 1, 5, -1, 8, 8, 10, 9, 14, 27, 26 ]
  -----------------        -----------------
     所有元素 < 8               所有元素 > 8

分治的关键在于，分治处理后主元恰好位于最终排好序后的位置上，其余元素则尚未排好序，只是简单地分置与主元两侧。快速排序正式（利用这一点）对数组不断进行分治操作，直至所有元素都位于正确的最终位置上。

在分治过程中，各个数值之间的相对顺序是无法保证的。所以在以 8 作为主元进行分治处理后，得到的数组也可能是这样的：

[ 3, 0, 5, 2, -1, 1, 8, 8, 14, 26, 10, 27, 9 ]

唯一可以保证的是，所有小于主元的数值全部位于左侧，而位于右侧的所有数值都大于它。但是由于分治处理会改变两个相等元素之间的原有顺序，所以快速排序不是一个稳定的排序算法（这一点与归并排序（merge sort）不同）。就大多数场景而言，这一点并不重要。

稳定排序的意义：以淘宝商品列表为例，列表可以按价格、好评、卖家区域等条件排序，可单选，也可多选。如果排序算法不稳定，先按价格排序，之后在追加好评和买家等排序条件时，原来符合追加条件的价格相同的商品的先后顺序就可能发生变化，这显然不是我们想要的。而稳定的排序算法就没有该问题。

Lomuto 分治策略

在第一个展示的例子中，由于是通过对 Swift filter() 函数的三次调用来实现的分治处理，这导致（算法）不够高效。所以我们得找一个能原位操作，即直接修改原始数组的分治算法。

下面是一个 Lomuto 分治策略的 Swift 实现：

// 这也是《算法导论》中提到的第一个快排方案
func partitionLomuto<T: Comparable>(_ a: inout [T], low: Int, high: Int) -> Int {
  let pivot = a[high]

  var i = low
  for j in low..<high {
    if a[j] <= pivot {
      (a[i], a[j]) = (a[j], a[i])
      i += 1
    }
  }

  (a[i], a[high]) = (a[high], a[i])
  return i
}

在 playground 中的测试代码如下：

1
2
3

var list = [ 10, 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1, 8 ]
let p = partitionLomuto(&list, low: 0, high: list.count - 1)
list  // 显示结果

注意 list 必须是可变的 var，因为 partitionLomuto() 需要对数组（以 inout 参数传入）的内容进行直接修改。这样就比每次都创建一个新数组要高效多了。

为了避免每次都从头开始对整个数组进行分治处理，low 和 high 两个参数是必不可少的，只有限定了范围才能逐步缩小它。

先前我们使用位于数组正中位置的元素作为主元，而 Lomuto 算法则总是使用末位元素 a[high] 作为主元，认清这点差异非常关键。鉴于之前我们一直使用 8 作为主元，所以这次我们将 8 和 26 的位置进行交换，让 8 位于数组末尾，依然被选为主元。
Previously we used the middle array element as the pivot but it’s important to realize that the Lomuto algorithm always uses the last element, a[high], for the pivot. Because we’ve been pivoting around 8 all this time, I swapped the positions of 8 and 26 in the example so that 8 is at the end of the array and is used as the pivot value here too.

译者注：对这段有点糊涂，没理解到作者的初衷。

分治处理后的数组：

[ 0, 3, 2, 1, 5, 8, -1, 8, 9, 10, 14, 26, 27 ]
                        *

变量 p 包含的是调用 partitionLomuto() 函数后的返回值 7。它是主元在新数组中的索引（以星号标记）。

0 到 p-1 的 [ 0, 3, 2, 1, 5, 8, -1 ] 构成了左半边。p+1 到末尾的 [ 9, 10, 14, 26, 27 ] 构成了右半边（此时右侧恰好已经排好序了）。

你可能已经注意到了一个比较有趣的情况…那就是 8 在数组中出现了不止一次。其中一个 8 并没有紧邻中间位于左半边的末位，所以这对 Lomuto 算法来说，是一个小小的不利，重复的元素越多，对于快速排序越不利。

那么 Lomuto 算法是如何运行的呢？关键就位于 for 循环。它将数组分成四个区域：

a[low...i] 所有 <= 主元的元素
a[i+1...j-1] 所有 > 主元的元素
a[j...high-1] 那些尚未查验的元素
a[high] 主元

⚠️ 译者注： 这里原作者表述有误，不是 for 循环将数组分成四部分，而是 for + swap(i, high) 将数组分成这四部分，否则你会发现起止索引对不上。

分治拆分后的四个区域如下：

[ values <= pivot | values > pivot | not looked at yet | pivot ]
  low           i   i+1        j-1   j          high-1   high

循环会从 low 到 high-1 遍历查验每个元素，如果该元素的值小于等于主元，就通过交换将它移到第一个区域。

注意： 在 Swift 中，(x, y) = (y, x) 是对 x 和 y 进行交换的一个便利操作，与使用 swap(&x, &y) 是完全等价的。

译者注：与 Array.swapAt(i, j) 相比较，没感觉有任何优势。见仁见智吧！

循环结束后，主元仍然位于数组的末位，所以我们需要将它与大于部分的首元素进行交换。此时主元正好位于小于等于与大于它的两部分的中间，数组的分治处理结束。

继续看例子。此时数组是这样的：

[| 10, 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
   low                                       high
   i
   j

初始时，从索引 0 到 11 为“未查验”区域，主元位于索引 12。由于查验尚未开始，所以 “values <= pivot” 和 “values > pivot” 的区域均为空。

看第一个元素，10。是否小于主元？否，跳至下一个元素。

[| 10 | 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
   low                                        high
   i
       j

现在“未查看”区域变成了 1 到 11，”values > pivot” 的区域也包含了一个数字 10，而 “values <= pivot” 到区域依然为空。

在查看第二个数值，0。是否比主元小呢？是，那么将 10 和 0 进行交换，并且将 i 向前移动一位。

[ 0 | 10 | 3, 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
  low                                         high
      i
           j

此时“未查验”区域变成了 2 到 11，”values > pivot”的区域还是只包含 10，而”values <= pivot”的区域则多了个 0。

继续查看第三个数值，3。比主元小，所以与 10 交换后得到：

[ 0, 3 | 10 | 9, 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
  low                                         high
         i
             j

“values <= pivot”的区域变成了 [ 0, 3 ]。继续查看…。9 比主元大，所以跳过：

[ 0, 3 | 10, 9 | 2, 14, 26, 27, 1, 5, 8, -1 | 8 ]
  low                                         high
         i
                 j

这是”values > pivot”的区域变成了 [ 10, 9 ]。如果按此操作继续，那么最终结果会是：

[ 0, 3, 2, 1, 5, 8, -1 | 27, 9, 10, 14, 26 | 8 ]
  low                                        high
                         i                   j

还有最后一件事要做，那就是通过交换 a[i] 和 a[high]，将主元放回原位
The final thing to do is to put the pivot into place by swapping a[i] with a[high]:

[ 0, 3, 2, 1, 5, 8, -1 | 8 | 9, 10, 14, 26, 27 ]
  low                                       high
                         i                  j

此外还返回了 i，主元的索引。

注意： 如果你对该算法的工作原理还是不完全明白，那么我建议你到 playground 中亲自尝试一番，在循环过程中，仔细观察一下这四个区域是如何创建的。

我们以此分治策略来构建一个快速排序。代码如下：

func quicksortLomuto<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
  if low < high {
    let p = partitionLomuto(&a, low: low, high: high)
    quicksortLomuto(&a, low: low, high: p - 1)
    quicksortLomuto(&a, low: p + 1, high: high)
  }
}

现在是不是一下简单很多。我们首先调用 partitionLomuto() 函数，以数组的最后一个元素为主元，对数组进行重排。然后在对左右两部分递归调用quicksortLomuto()，进行排序。

测试一下:

1 2	var list = [ 10, 0, 3, 9, 2, 14, 26, 27, 1, 5, 8, -1, 8 ] quicksortLomuto(&list, low: 0, high: list.count - 1)

Lomuto 策略并不是唯一的分治策略，虽然与交换操作更少的 Hoare 分治策略相比，效率上略逊一筹，但它却是最容易理解的。

Hoare 分治策略

该分治方案由快速算法的发明者 Hoare 创建。

代码如下：

func partitionHoare<T: Comparable>(_ a: inout [T], low: Int, high: Int) -> Int {
  let pivot = a[low]
  var i = low - 1
  var j = high + 1

  while true {
    repeat { j -= 1 } while a[j] > pivot
    repeat { i += 1 } while a[i] < pivot

    if i < j {
      a.swapAt(i, j)
    } else {
      return j
    }
  }
}

playground 测试代码如下:

1
2
3

var list = [ 8, 0, 3, 9, 2, 14, 10, 27, 1, 5, 8, -1, 26 ]
let p = partitionHoare(&list, low: 0, high: list.count - 1)
list  // show the results

注意在 Hoare 方案中，总是以数组的第一个元素，a[low] 作为主元。同样，我们还是以 8 作为主元。

结果如下:

[ -1, 0, 3, 8, 2, 5, 1, 27, 10, 14, 9, 8, 26 ]

注意此次主元并没有位于正中。与 Lomuto 方案不同，返回值，即主元在新数组中的索引，并不是必须的。

数组将被分成 [low...p] 以及 [p+1...high] 两部分。例如，返回值 p 是 6，那么这两部分将分别是 [ -1, 0, 3, 8, 2, 5, 1 ] 和 [ 27, 10, 14, 9, 8, 26 ]。

主元会位于其中的一个部分，但算法并没有指明是哪一个。如果数组内主元的值出现不止一次。那么在具体例子中，它既可能位于左半边，也可能位于右半边。

基于这点不同，Hoare 快速排序算法的实现也有些许差异：

func quicksortHoare<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
  if low < high {
    let p = partitionHoare(&a, low: low, high: high)
    quicksortHoare(&a, low: low, high: p)
    quicksortHoare(&a, low: p + 1, high: high)
  }
}

至于 Hoare 分治策略的详细步骤，我就把它当作练习，留给各位读者了。 :-)

译者注：练习时可以考虑下——在分治算法中，是否可以用 while 循环代替 repeat while 呢？

主元的选择

虽然 Lomuto 分治策略总是以末位元素作为主元，而 Hoare 策略则总是以首元素作为主元，但没有任何证据表明这么做有什么优势。

下面展示一下，如果选了一个糟糕的主元会如何。以如下数组为例：

[ 7, 6, 5, 4, 3, 2, 1 ]

采用 Lomuto 分治策略。主元为末位元素，1。经拆分，得到如下数组：

   less than pivot: [ ]
    equal to pivot: [ 1 ]
greater than pivot: [ 7, 6, 5, 4, 3, 2 ]

对“大于”部分递归，继续进行拆分：

   less than pivot: [ ]
    equal to pivot: [ 2 ]
greater than pivot: [ 7, 6, 5, 4, 3 ]

继续:

   less than pivot: [ ]
    equal to pivot: [ 3 ]
greater than pivot: [ 7, 6, 5, 4 ]

以此重复下去…

糟糕了，直接将快速排序降级成插入排序了。为了让快速排序更效率，（在分治过程中）需要尽可能的将数组进行平分。

在这个例子中，最优的主元应该是 4，这样可以得到：

   less than pivot: [ 3, 2, 1 ]
    equal to pivot: [ 4 ]
greater than pivot: [ 7, 6, 5 ]

那么是不是选择中间元素就一定比首末元素更好呢？试着看下这个例子：

[ 7, 6, 5, 1, 4, 3, 2 ]

此时中间元素是 1，如果以它为主元，那么得到结果会跟之前的例子一样糟糕。

理想的主元应该是待分数组的中位数，也就是位于有序数组正中的那个元素。然而，排序之前，你又不可能知道。所以这有点像先有鸡还是先有蛋的问题。尽管如此，我们还有一些技巧可以选择一个相对较好的主元。

其中一个技巧是，取“三元素的中位数”，即子数组首、中、末三个元素的中位数。理论上而言，它通常是最接近真实中位数的。

另一个常见的解决方案是随机选择主元。虽然有时选中的主元不怎么理想，但平均而言，这是一个非常不错的选择。

下面是一个通过随机方式挑选主元的快速排序算法：

func quicksortRandom<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
  if low < high {
    let pivotIndex = random(min: low, max: high)         // 1

    (a[pivotIndex], a[high]) = (a[high], a[pivotIndex])  // 2

    let p = partitionLomuto(&a, low: low, high: high)
    quicksortRandom(&a, low: low, high: p - 1)
    quicksortRandom(&a, low: p + 1, high: high)
  }
}

与之前相比有两点重要区别：

random(min:max:) 函数会返回一个位于 min...max 区间内的整数，作为主元的索引。
由于 Lomuto 分治策略总是以 a[high] 作为主元，所以在调用 partitionLomuto() 之前，我们先对a[pivotIndex] 和 a[high] 进行交换，以便将主元放置末位。

虽然在排序算法中使用随机数有点怪，但为让快速排序在所有情况下都相对高效，这一操作就是必不可少的。一个糟糕的主元可以让快速排序的时间复杂度飙至 **O(n^2)**，而如果你借助来随机数生成器，通常都能选择一个较好的主元，那么它的时间复杂度就会变为 **O(n log n)**，这样的排序算法就相当不错了。

荷兰旗分治法（Dutch national flag partitioning）

算法仍有改进的余地！在第一个展示的例子中，数组最终被分治成如下样式：

[ values < pivot | values equal to pivot | values > pivot ]

But as you’ve seen with the Lomuto partitioning scheme, if the pivot occurs more than once the duplicates end up in the left half. And with Hoare’s scheme the pivot can be all over the place. 面对此种情况的解决方案就是“荷兰旗分治策略”，这个名字源自荷兰国旗由三部分构成，就像我们也要将数组分成三部分一样。

该分治策略的代码实现如下:

func partitionDutchFlag<T: Comparable>(_ a: inout [T], low: Int, high: Int, pivotIndex: Int) -> (Int, Int) {
  let pivot = a[pivotIndex]

  var smaller = low
  var equal = low
  var larger = high

  while equal <= larger {
    if a[equal] < pivot {
      swap(&a, smaller, equal)
      smaller += 1
      equal += 1
    } else if a[equal] == pivot {
      equal += 1
    } else {
      swap(&a, equal, larger)
      larger -= 1
    }
  }
  return (smaller, larger)
}

在工作原理上，它除了与 Lomuto 分治策略中将数组分成的四个区域不同外，其它非常类似：

[low ... smaller-1] 包含所有 values < pivot
[smaller ... equal-1] 包含所有 values == pivot
[equal ... larger] 包含所有 values > pivot
[larger ... high] 尚未查验的数值

注意，它并不假定 a[high] 为主元，相反，你必须传入一个欲将其作为主元的元素的索引。

一个应用的例子:

1
2
3

var list = [ 10, 0, 3, 9, 2, 14, 8, 27, 1, 5, 8, -1, 26 ]
partitionDutchFlag(&list, low: 0, high: list.count - 1, pivotIndex: 10)
list  // show the results

为了好玩，这里我们给出另一个 8 的索引。如下：

[ -1, 0, 3, 2, 5, 1, 8, 8, 27, 14, 9, 26, 10 ]

注意两个 8 此时在数组中的位置。partitionDutchFlag() 的返回值是一个元组，(6, 7)。正好是主元在数组中的索引范围。

怎么在快速排序中应用呢：

func quicksortDutchFlag<T: Comparable>(_ a: inout [T], low: Int, high: Int) {
  if low < high {
    let pivotIndex = random(min: low, max: high)
    let (p, q) = partitionDutchFlag(&a, low: low, high: high, pivotIndex: pivotIndex)
    quicksortDutchFlag(&a, low: low, high: p - 1)
    quicksortDutchFlag(&a, low: q + 1, high: high)
  }
}

如果数组中包含多个重复元素，使用荷兰国旗分治策略可以让快速排序更高效。（绝对不是因为我是荷兰人，才这么说哦）

注意： 上面给出的 partitionDutchFlag() 实现中，使用了自定义的 swap() 例程，来交换两种数组中的元素。与 Swift 自带的 swap() 不同，当两个索引指向同一个数组的元素时，它不会报错。详情参见 Quicksort.swift 代码

最后

该系列文章翻译自 Raywenderlich 的开源项目：swift-algorithm-club。受限于译者英语水平及翻译经验，译文难免有词不达意，甚至错误的地方，还望不吝赐教，予以指正

参见

Quicksort on Wikipedia

由 Matthijs Hollemans 为 Swift 算法社区撰写

由 William Han 翻译