【译】数据结构与算法——堆

发表于 更新于 分类于

堆实际上是一个内部元素以二叉树（binary tree）形式存储的数组（译者：必须是完全二叉树），且无需父/子（节点）指针。堆是基于堆属性（heap property）存储的，堆属性决定了其子节点在树中的排序。（译者：堆属性也称为堆特征主要是指堆内元素的排序方式）

堆的常用场景：

堆属性（The heap property）

有两种堆：大序堆 和 小序堆，他们之间最大的区别就在于子节点在树中的排序不同。（译者：也有译为大顶堆和小顶堆，最大堆和最小堆的。这里将 max-heap 和 min-heap 译为大序堆和小序堆，是为了突出他们最大的区别——排序）

在大序堆中，父节点的值要比其所有字节点的值都大。在小序堆中，每个父节点的值都要小于其子节点的值。这被称为“堆属性”，并且它适用于树中的每个节点。

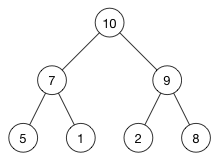
例如：

A max-heap

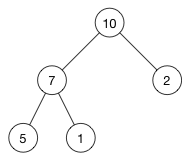
这是一个大序堆，每个父节点都比其所有的子节点大。(10) 大于 (7) 和 (2). (7) 大于 (5) 和 (1)。

受限于堆属性，大序堆总是将最大的对象作为树的根。反之，小序堆总是将最小的对象作为其树的根。正是因为堆有这样的属性，所以通常用它来实现优先队列（priority queue） ，以便更快捷的获取那个“最重要”的对象。

注意: 堆的根不是最大就是最小值，但是后续的其它元素顺序是无法保证的。例如，大序堆中索引为 0 的元素一定是最大的，但这并不意味着最后一个索引位元素就是最小的。只能保证最小值在其叶子节点中，但无法确定是哪一个。

堆与其它常见树有什么不同

堆不能取代二叉搜索树，他们之间既有相似也有不同。下面是它们之间的主要区别：

节点顺序 在二叉搜索树（binary search tree——BST）中，左侧的子节点必须小于父节点，而右侧的子节点则必须大于父节点。而堆无此要求。大序堆中两个子节点都必须小于父节点，而小序堆则必须都大于父节点。

内存占用 传统树所耗内存比其实际存储数据要大一些。你需要开辟外的存储空间以存储节点对象和指向左右子节点的指针。堆则使用普通的数组作为存储结构，且不需要（额外的）指针。

平衡性 二叉搜索树必须是“平衡”的，这样大多数操作才具有 O(log n) 的时间杂度。因此你必须以完全随机的方式插入或删除数据，否则就要用平衡树（AVL tree） 或 红黑树（red-black tree）（以保持其平衡性）。而堆不需要整棵树都是有序的，只要堆属性完备即可，因此不存在平衡性的问题。堆 O(log n) 的时间杂度是有堆自身树觉结构决定的。

查询 二叉树的搜索很快，堆较慢。相对于在堆前端添加最大（或最小）值，以及允许快速插入和删除等特性，查询的优先级则不那么高。

数组中的树

用数组去实现一个树形结构，虽然听上去是有点奇怪，但是在时间和空间上都非常高效。

前面的例子如果用树来存储，形式如下：

[ 10, 7, 2, 5, 1 ]

这就是全部了，完全不需要比数组更多的存储空间。

既然没有额外指针，怎么确定哪个是子节点，那个父节点呢？好问题！（实际上）树中各节点在数组中的索引顺序已经定义好了其间的父子关系。

假定 i 是某节点的索引，那么通过下面的公式就可以求得相应父节点和子节点的索引：

parent(i) = floor((i - 1)/2)
left(i)   = 2i + 1
right(i)  = 2i + 2

注意， right(i) 仅仅是 left(i) + 1。因为左右节点总是相邻存储在一起。

将数组的相应索引带入上面的公式，就可以得到父节点和子节点对应的位置：

节点 数组索引 (i) 父索引 左子节点 右子节点
10 0 -1 1 2
7 1 0 3 4
2 2 0 5 6
5 3 1 7 8
1 4 1 9 10

检查一下，确认数组索引与图中所示的树是不是一一对应的。

注意： 根节点 (10) 没有父节点，因为 -1 不是一个有效的数组索引。同理， 节点 (2), (5) 和 (1) 也不存在子节点，因为它们的数组索引越界了，由此可见，在使用前，务必要先确认索引的有效性。

回想一下大序堆，父节点的值必须使用大于（或等于）子节点的值。也就是说下面的（表达式）对数组中的所有索引 i 都必须为 true：

1
array[parent(i)] >= array[i]

确认一下，例子中给出的堆是否保持了该堆属性。

可见，该方程可以使我们不通过指针也能找到相应的父节点或子节点的索引。相比指针（的方式）复杂一些，但权衡利弊：虽增加了计算量，但也节约了内存空间。幸运地是，该计算方式够快，且时间复杂度为 O(1) 。

理解数组中索引与树中节点位置的映射关系非常重要。（例如）下面是一棵分为 4 层含有 15 个节点的树：

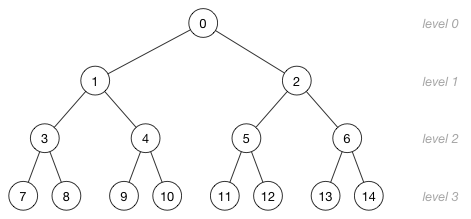
Large heap

图中的数字并不是节点的值，而是（节点）对应在数组中的索引。下面给出了数组索引与树不同层级之间的对应（关系）：

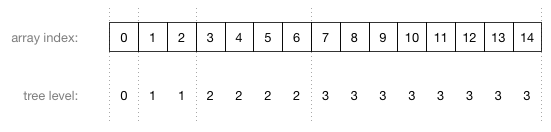
The heap array

要想公式有效，数组中的父节点必须位于子节点之前。可以上之前的图中印证（这一点）。

注意这种方式是有限制的。（例如）下图就必须用常规的二叉树，而不能用堆：

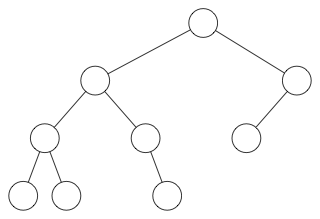
Impossible with a heap

在当前最底层的节点被占满之前，是不可以生成新的一层的，所以堆的形状始终是下面这样：

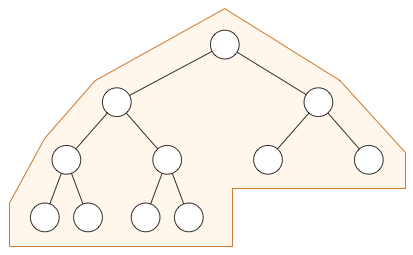
The shape of a heap

注意： 你可以用堆的形式去遍历一个普通二叉树，只是这样不仅浪费空间，而且还需要把数组中空值标记出来。（译者：因为普通的二叉树的一层未必是满的）

突击测验！假设我们有下面这样一个数组：

[ 10, 14, 25, 33, 81, 82, 99 ]

它是一个有效的堆吗？是的！一个从小到大的有序数组就是一个有效的小序堆。可以向下面这样把它画出来：

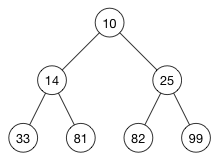
A sorted array is a valid heap

由于父节点总是小于它对子节点，因此堆属性得以维系。(自己确认下，一个从大到小的的有序数组是不是一个有序的大序堆)

注意： 不是所有的小序堆都是一个有序的数组！它是不可逆的。要想把堆变为有序数组，需要借助堆排（heap sort）

更多的数学

如果你很好奇，那么这里还有一些公式可以更好的表现堆的属性（特征）。你不需要理解的很透彻，但它有时却真的可以派上用场。该小节可以跳过。(译者：翻译不够好，有待更新，原文暂时保留)
In case you are curious, here are a few more formulas that describe certain properties of a heap. You do not need to know these by heart, but they come in handy sometimes. Feel free to skip this section!

树的高度定义了从根部到最底部的叶子节点所需的跳数，或者更公式化一点说：高度就是节点间的最大边数。h 高度 h 的堆拥有 h+1 层。

下面的堆高度是 3， 所以他有 4 层：

Large heap

一个包涵 n 个节点的堆，其高度是 *h = floor(log2(n))*。之所以如此，是因为在添加新层之前，总是先把上一层级的节点添满。例子中有15个节点，所以它的高度是 floor(log2(15)) = floor(3.91) = 3。

如果最底层已经填满，那么这一层包涵 2^h 个节点。余下的树上层包涵 2^h - 1 个节点。带入例子中相应的数据：最低一层有 8 个节点，恰好是 2^3 = 8。前面的三层共包含 7 个节点，正好等于 2^3 - 1 = 8 - 1 = 7。

整个堆中节点总数是 2^(h+1) - 1。代入例子，2^4 - 1 = 16 - 1 = 15。

一个高度为 h 含有 n 个元素堆，最多可以拥有 ceil(n/2^(h+1)) 个节点。（译者：这里没懂，有待更新）
There are at most ceil(n/2^(h+1)) nodes of height h in an n-element heap.

叶子节点在数组中的索引范围总是 floor(n/2) 到 n-1。由此我们可以快速地通过数组来构建一个堆。如有疑问，可以通过例子来验证这一结论。;-)

几个简单的数学知识照亮了你的一天。（译者：这句翻译的极差，原文暂时保留。）
Just a few math facts to brighten your day.

能用堆做什么呢？

在插入或移除元素后，有两个基本操作必须要做，以保证堆是一个有效的大序堆或小序堆：

  • shiftUp(): 如果某个元素大于 (大序堆) 或小于 (小序堆) 它的父（节点）, 那么它就需要与父节点进行交换. 使它在整个树中上移。

  • shiftDown(). 如果某个元素小于 (大序堆) 或大于 (小序堆) 它的子节点, 它就需要在整个树中下移。 这一操作也被称为 “堆化（heapify）”.

上移或下移是个递归程序，其时间复杂度都是 **O(log n)**。

下面是一些构建于基础操作之上的操作：

  • insert(value): 在堆末端添加一个新元素，之后在通过 shiftUp() 对堆进行恢复（译者：恢复堆属性，回想下为什么要这么做）

  • remove(): 移除并返回最大值（大序堆）或最小值（小序堆），会导致堆出现空缺（译者：根位置），要填上这个空位，首先将最后一个元素填补到根的位置，之后在通过 shiftDown() 操作来恢复堆属性。（有时该操作也被称为“取小（extract min）”或“取大（extract max）”）

  • removeAtIndex(index): 类似 remove()， 区别就在于，除了根元素，它还允许你移除任意堆内其它元素。该（方法）同样会在新晋元素与其子元素顺序错误时或者新晋元素与其父元素顺序错误时调用到 shiftDown() 和 shiftUp() （方法）。

  • replace(index, value): 给一个 (小序堆)的节点赋相对更小的值或给一个 (大序堆) 的节点赋相对更大的值时， 由于该操作会破坏堆属性, 所以之后会通过 shiftUp() 方法进行恢复（译者：恢复堆的排序属性）. (也称为 “decrease key” 和 “increase key”.)

因为无论是升档 shiftUp() 还是降档 shiftDown() 都是昂贵的操作，所以以上操作的时间杂度都是 O(log n) 。此外还有一些操作更耗时：

  • search(value). 堆（结构）本身就不是为了高效查询而建立的, 但是因为 replace() 和 removeAtIndex() 操作需要查询目标节点的索引, 所以不得不如此。 时间杂度: **O(n)**。

  • buildHeap(array): 通过反复调用 insert() 方法，将一个（无序）数组转化为堆。如果你做的够好，那么（该方法的）时间杂度应该是 **O(n)**。

  • 堆排（Heap sort）. 鉴于堆是一个数组, 我们可以借助一特点对其进行从低到高地排序。 时间杂度: **O(n lg n)**。

堆还有一个 peek() 方法，可以返回最大（大序堆）或最小（小序堆）的元素，而无需从堆中移除。时间杂度：**O(1)**。

注意: 虽然说了这么多，但是最常用的还是插入新元素 insert() 和移除最大或最小值的remove() 两个操作。它们的时间杂度都是 **O(log n)**。其它操作都是为了一些进阶应用，例如在构建优先级队列时，可以对已添加的重要对象进行修改。

向堆中插入

下面我们通过一个插入的例子来深入了解这一操作过程。以插入 16 为例：

The heap before insertion

与之对应的数组是 [ 10, 7, 2, 5, 1 ].

首先将要插入的元素添加至数组末尾，此时数组变为：

[ 10, 7, 2, 5, 1, 16 ]

对应的树如下：

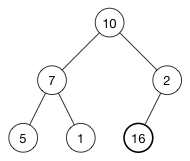
The heap before insertion

(16) 被添加到了最后一行的第一个有效位。

如此堆属性被破坏了，因为 (2) 排在了 (16) 上面，而正确的应该是是大数在小数上面。（这是大序堆）

要恢复堆属性，我们需要将 (16) 和 (2) 互换。

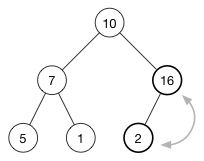
The heap before insertion

还没完，因为 (10) 还是比 (16) 小。继续将其与父元素进行交换，直至父元素更大或者抵达数的顶端。该（操作）被称为 升档（shift-up） 或者 换挡（sifting），每次插入都会被执行。使得哪些比较大或比较小的数沿着树“上浮”。

最终结果如下：

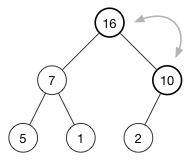
The heap before insertion

现在每个父节点都比其子节点要大了。

由于升档所耗费的时间与树的高度是成正例的，所以它的时间杂度是 **O(log n)**。（向数组末尾添加元素的时间杂度仅仅是 **O(1)**，所以它对总体的时间杂度无影响。）

移除根

从树中移除 (10)：

The heap before removal

空出来的顶点会怎么样呢？

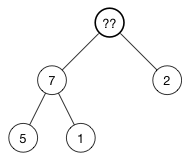
The root is gone

插入时，我们是将新值添加到数组末尾。这次反过来：取到最后一个元素，在将它放到树的顶端，然后在（逐步）恢复堆属性。

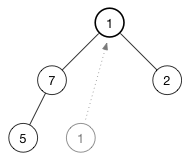
The last node goes to the root

我们来看看怎么对 (1) 进行 降档（shift-down）。要恢复大序堆的堆属性，需要最大的值在顶端。此时有两个候选交换对象： (7) 和 (2)需要交换。选择三个节点中最大的。也就是 (7)（进行交换），交换(1) 和 (7) 后如下图

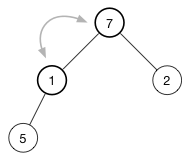
The last node goes to the root

继续将挡，直到该节点没有子节点，或者它比其所有子节点都大。对我们这个堆来说，再进行一次交换即可恢复堆属性：

The last node goes to the root

升降操作的次数与树的高度是正比的，其时间杂度是 **O(log n)**。

注意： 无论 shiftUp() 还是 shiftDown() 一次都只能恢复那些只有一个元素位置错误的（堆）。 如果有多个元素位置错误，那么就需要每个错误元素都调用一次该方法。

移除任意节点

鉴于堆的设计初衷，大多数时间我们都只是需要移除根元素。

然而，随机移除某个元素也非常有帮助。这个一个通用版的 remove()，并且需要调用 shiftDown() 或 shiftUp() 方法。

还是用之前的例子，来移除 (7)：

The heap before removal

初始，数组是这样的：

[ 10, 7, 2, 5, 1 ]

如你所知，移除一个元素会潜在的破坏大序堆或小序堆属性。要修复这点，我们需要将最后一个元素与我们即将移除的元素做交换。

[ 10, 1, 2, 5, 7 ]

最后一个元素是我们需要返回的元素；接下来通过 removeLast() 方法将其从堆中移除。此时 (1) 因为比它的子节点 (5) 小，所以是错序的。通过 shiftDown() 来修正。

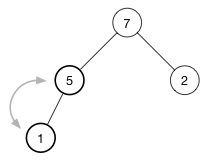
然而，光降档可不够应对所有情况，还有可能需要升档。试想一下如果从下面的堆中移除 (5)：

We need to shift up

(5) 跟 (8) 交换。此时由于 (8) 比其父节点要大，所以需要进行 shiftUp()。

通过数组创建堆

数组转堆很方便，只要将数组中的元素按堆属性进行排序即可。

代码是如下：

1
2
3
4
5
private mutating func buildHeap(fromArray array: [T]) {
  for value in array {
    insert(value)
  }
}

只是简单地对数组中的每个元素调用了 insert() 方法。简单是简单，但不够效率。由于要对 n 个元素逐个执行 log n 插入操作，所以它的时间杂度是 **O(n log n)**。

如果前一节的数学“buff”还在，你就会发现，任何位于数组 n/2 到 n-1 索引位的堆元素都是树的叶子节点。这部分完全可以跳过，只处理其余节点即可，那怕他们可能是一个或多个子节点的父节点，甚至顺序错误。

代码：

1
2
3
4
5
6
private mutating func buildHeap(fromArray array: [T]) {
  elements = array
  for i in stride(from: (nodes.count/2-1), through: 0, by: -1) {
    shiftDown(index: i, heapSize: elements.count)
  }
}

Here, elements is the heap’s own array. We walk backwards through this array, starting at the first non-leaf node, and call shiftDown(). This simple loop puts these nodes, as well as the leaves that we skipped, in the correct order. This is known as Floyd’s algorithm and only takes O(n) time. Win!（译者注：这里还要补充一下弗洛伊德算法的知识，在更新。）

堆搜索

堆就不是为了搜索而建立的，但是如果你想通过 removeAtIndex() 随机移除一个元素或者通过 replace() 随机的修改一个元素，那么就需要先获取该元素的索引。查询也便成了必然，即使很慢。

在二叉搜索树（binary search tree）中，由于节点间固有的顺序特征，所以检索的速度非常快。然而堆节点的排序与之是不同的，所以二叉搜索算法（此时）行不通，我们必须遍历树中的每个节点。

再次以之前的堆为例：

The heap

假设我们要查找节点 (1) 的索引，此时必须线性搜索遍历整个数组 [ 10, 7, 2, 5, 1 ]

即使堆属性在建立时没有考虑到搜索，但我们还是可以利用到一些它的特点。鉴于大序堆中的父节点总是比其子节点大，因此如果父节点比查找的目标值还小，那么我们就可以忽略其子节点（和子节点的子节点，以及其子子孙孙）

假设我们要查看堆是否包含数值 8 (不存在）。首先从根节点 (10)开始。根不是，之后递归他的左右子节点。左节点是 (7)，不是我们要找的，但鉴于是一个大序堆，所以 (7) 的子节点也不用找了。因为他们都比 7 小，永远也不可能等于 8。同理，右节点的 (2)也是如此。

尽管有些小的优化，但是搜索的时间杂度依然是 **O(n)**。

注意： 可以用一个额外的字典来保存节点值与其索引的映射关系，如此搜索的时间杂度可以降为 **O(1)**，如果经常需要修改优先队列（priority queue）中元素的“优先级”，且该优先队列是构建在堆之上的，那么这这么做还是非常值得的。（译者：牺牲空间换取时间）

代码

请参见Heap.swift，以了解该概念是如何通过 Swift 实现的。绝大部分代码都非常直观。稍微有点技巧的点在 shiftUp() 和 shiftDown() 方法中。

有两种类型的堆：大序堆和小序堆。他们唯一的区别就是排序方式：大值在先还是小值在先。

相比于创建两个不同版本的堆，MaxHeap 和 MinHeap，这里只有一个 Heap 对象，只是它还可以接受一个 isOrderedBefore 闭包。该闭包包含判断两个值大小的逻辑。可能你很早就接触，因为它也被用在 Swift 的 sort() 方法中。

创建在一个整形的大序堆：

1
var maxHeap = Heap<Int>(sort: >)

创建相应的小序堆:

1
var minHeap = Heap<Int>(sort: <)

I just wanted to point this out, because where most heap implementations use the < and > operators to compare values, this one uses the isOrderedBefore() closure.

参见

堆_维基百科

最后

该系列文章翻译自 Raywenderlich 的开源项目：swift-algorithm-club，意在帮助有一定算法基础的同学进行回顾，如果你才接触算法，那么建议移步阅读详细教程

由 Kevin Randrup 和 Matthijs Hollemans 联合发表于 Swift 算法社区

由 William Han 翻译