【译】数据结构与算法——二叉树

二叉树是一种特殊的树（tree），它的每个节点只能有 0， 1 或 2 个子节点。

下面是一个二叉树：

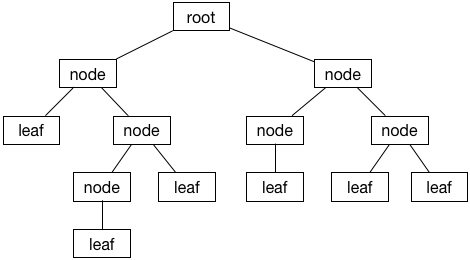
子节点通常分为 左 和 右 子节点。如果一个节点没有任何子节点，那么它被称为 叶子 子节点。根 指位于树最顶端的节点。

通常节点有一个指向父节点的（指针/引用），但不是必须的。

二叉树中应用最广泛的是二叉搜索树（binary search trees）。它的节点以特定顺序排列（小值在左，大值在右）。当然不是所有的二叉树都必须如此。

例如，下面的二叉树，它展示的是一则算术运算 (5 * (a - 10)) + (-4 * (3 / b)) ：

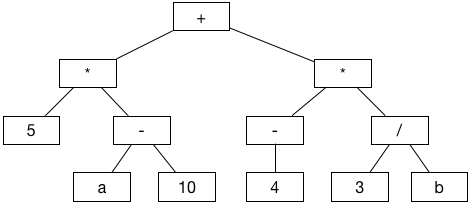
代码

下面通过 Swift 实现了一个通用二叉树:

public indirect enum BinaryTree<T> {
  case node(BinaryTree<T>, T, BinaryTree<T>)
  case empty
}

怎么用呢？下面用它来构建一则算术运算：

// leaf nodes
let node5 = BinaryTree.node(.empty, "5", .empty)
let nodeA = BinaryTree.node(.empty, "a", .empty)
let node10 = BinaryTree.node(.empty, "10", .empty)
let node4 = BinaryTree.node(.empty, "4", .empty)
let node3 = BinaryTree.node(.empty, "3", .empty)
let nodeB = BinaryTree.node(.empty, "b", .empty)

// intermediate nodes on the left
let Aminus10 = BinaryTree.node(nodeA, "-", node10)
let timesLeft = BinaryTree.node(node5, "*", Aminus10)

// intermediate nodes on the right
let minus4 = BinaryTree.node(.empty, "-", node4)
let divide3andB = BinaryTree.node(node3, "/", nodeB)
let timesRight = BinaryTree.node(minus4, "*", divide3andB)

// root node
let tree = BinaryTree.node(timesLeft, "+", timesRight)

构建树时要反着来，首先从叶子节点开始，然后向上直至顶端。

添加一个 description 方法，以便打印整个树：

extension BinaryTree: CustomStringConvertible {
  public var description: String {
    switch self {
    case let .node(left, value, right):
      return "value: \(value), left = [\(left.description)], right = [\(right.description)]"
    case .empty:
      return ""
    }
  }
}

print(tree) 打印输出如下：

value: +, left = [value: *, left = [value: 5, left = [], right = []], right = [value: -, left = [value: a, left = [], right = []], right = [value: 10, left = [], right = []]]], right = [value: *, left = [value: -, left = [], right = [value: 4, left = [], right = []]], right = [value: /, left = [value: 3, left = [], right = []], right = [value: b, left = [], right = []]]]

适当调整下缩紧，在带点联想，树的结构应该是这样的：

value: +, 
    left = [value: *, 
        left = [value: 5, left = [], right = []], 
        right = [value: -, 
            left = [value: a, left = [], right = []], 
            right = [value: 10, left = [], right = []]]], 
    right = [value: *, 
        left = [value: -, 
            left = [], 
            right = [value: 4, left = [], right = []]], 
        right = [value: /, 
            left = [value: 3, left = [], right = []], 
            right = [value: b, left = [], right = []]]]

另一个有用的方法就是统计树中的节点数：

public var count: Int {
  switch self {
  case let .node(left, _, right):
    return left.count + 1 + right.count
  case .empty:
    return 0
  }
}

以上面给的例子为例, tree.count 应该为 12.

经常需要对二叉树进行，如以某种特定顺序查看所有节点。常用的遍历方法有三种（译者：主要是依据根节点的查询位置确定先、中、后序遍历）：

1. 中序遍历（In-order）（也称 深度优先（depth-first））：先遍历一个节点的左子节点，在遍历其自身，最终遍历其右子节点（译者：左根右，以下图为例应为：4、2、8、5、1、6、3、7）。
2. 前序遍历（Pre-order）：先遍历一个节点自身，在遍历其左子节点，和右子节点（译者：根左右，以下图为例应为：1、2、4、5、8、3、6、7）。
3. 后序遍历（Post-order）：先遍历左和右子节点，在遍历节点自身（译者：左右根，以下图为例应为：4、5、8、2、3、6、7、1）。

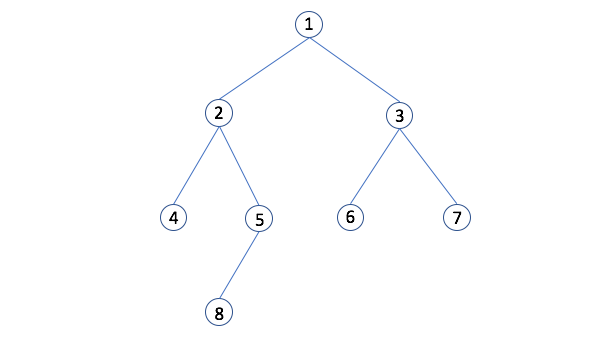
注意：这里给出的中、先、后序遍历解释太简单了，不足以理解(至少译者理解不能)，所以译者补了一个插图和相应的实例，非原文内容。当然最好的理解方式还是上手亲自跑一遍代码。

下面是实现代码:

public func traverseInOrder(process: (T) -> Void) {
  if case let .node(left, value, right) = self {
    left.traverseInOrder(process: process)
    process(value)
    right.traverseInOrder(process: process)
  }
}

public func traversePreOrder(process: (T) -> Void) {
  if case let .node(left, value, right) = self {
    process(value)
    left.traversePreOrder(process: process)
    right.traversePreOrder(process: process)
  }
}

public func traversePostOrder(process: (T) -> Void) {
  if case let .node(left, value, right) = self {
    left.traversePostOrder(process: process)
    right.traversePostOrder(process: process)
    process(value)
  }
}

在处理树结构时会经常用到，这中自己调用自己的函数称为递归。

例如，如果后序遍历之前的算术运算二叉树，那么其打印结果如下：

5
a
10
-
*
4
-
3
b
/
*
+

首先出现的叶子，最后出现的是根。

之后便可通过一个栈来计算该表达式, 类似下面的伪代码:

tree.traversePostOrder { s in 
  switch s {
  case this is a numeric literal, such as 5:
    push it onto the stack
  case this is a variable name, such as a:
    look up the value of a and push it onto the stack
  case this is an operator, such as *:
    pop the two top-most items off the stack, multiply them,
    and push the result back onto the stack
  }
  the result is in the top-most item on the stack
}

最后

该系列文章翻译自 Raywenderlich 的开源项目：swift-algorithm-club，意在帮助有一定算法基础的同学进行回顾。

由 Matthijs Hollemans 发表于 Swift 算法社区

由 William Han 翻译