【译】数据结构与算法——二叉搜索树

发表于 更新于 分类于

二叉搜索树是一种特殊的二叉树（每个节点最多拥有 2 个子节点），无论插入还是删除，它总是有序的。

要了更多关于树的知识，请先阅读这篇。

始终有序性

下面是一个二叉搜索树的示例:

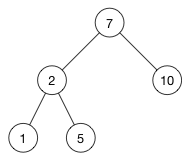
A binary search tree

注意每个左子节点都比父节点小，每个右子节点都比父节点大。这是一个二叉搜索树的关键特性。

例如, 2 小于 7, 所以它在左侧; 5 大于 2, 所以它在右侧.

节点的插入

当执行插入操作时，首先将要插入的值与根节点比较。如果该值较小，就取左分支；如果该值较大，就取右分支。如此沿着树向下比较，直至找到一个空位，将新增值插入。

假设我们要插入数值 9:

  • 从树的根开始 (该节点值为 7) 将其与 9 进行比较。
  • 9 > 7，所以取右分支，并继续与右子节点 10 进行比较。
  • 由于 9 < 10, 取左分支.
  • 现在已抵达无值可比的空位，所以将新节点 9 插入该位置。

下面是插入 9 以后的树：

After adding 9

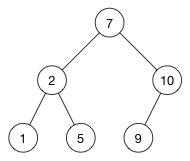
树中有且仅有一个位置可以插入该值。查找这个位置同行很快。时间杂度是 O(h)**，其中 **h 代表树的高度。

注意： 节点的高度是指从该节点到其最底层叶子节点的跳数。整个树的高度是指从根节点到最底层叶子节点到跳数。二叉搜索树的很多操作都通过树的高度来表示。

小值居左，大值居右，记住这个简单的规则，就可以让树始终保持有序，所以任何时候查询，都可以判断某个值是否包含在树中。

树的搜索

在树中搜索某个值，与插入操作步骤相同：

  • 如果该值小于当前节点，取左分支。
  • 如果该值大于当前节点，取右分支.
  • 如果该值等于当前节点，找到了!

与大多数树操作类似，这也递归操作，直至找到或者遍历完所有节点。

下面是一个搜索 5 的例子:

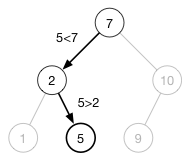
Searching the tree

通过树结构进行搜索非常快捷。耗时仅 **O(h)**。那怕你有一百万个节点，只要平衡性够好，也只需要 20 步便可找到。（思路非常类似数组中的二分搜索算法（binary search））

树的遍历

有时需要查看所有节点，而不是某一个。

遍历一个二叉树主要有三种方法:

  1. 中序遍历（In-order） (或者 深度优先遍历（depth-first）)：先查左子节点，在查父节点，最后查右子节点。
  2. 前序遍历（Pre-order）：先查父节点，在查左、右子节点。
  3. 后序遍历（Post-order）：先查左、右子节点，在查父节点。

树的遍历也是递归进行的。

如果以中序遍历一个二叉搜索树，那么所有节点就像是从小到大排列一样。例如下图，将依次打印 1, 2, 5, 7, 9, 10：

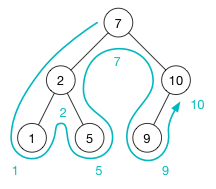
Traversing the tree

节点的移除

移除节点非常简单。移除后，需要用其左分支上最大的子节点或右分支上最小的子节点填充其位置。如此就能在移除后依然保持有序性。例如下图，移除 10 后需要用 9（图2） 或者 11（图3） 填充其位置。

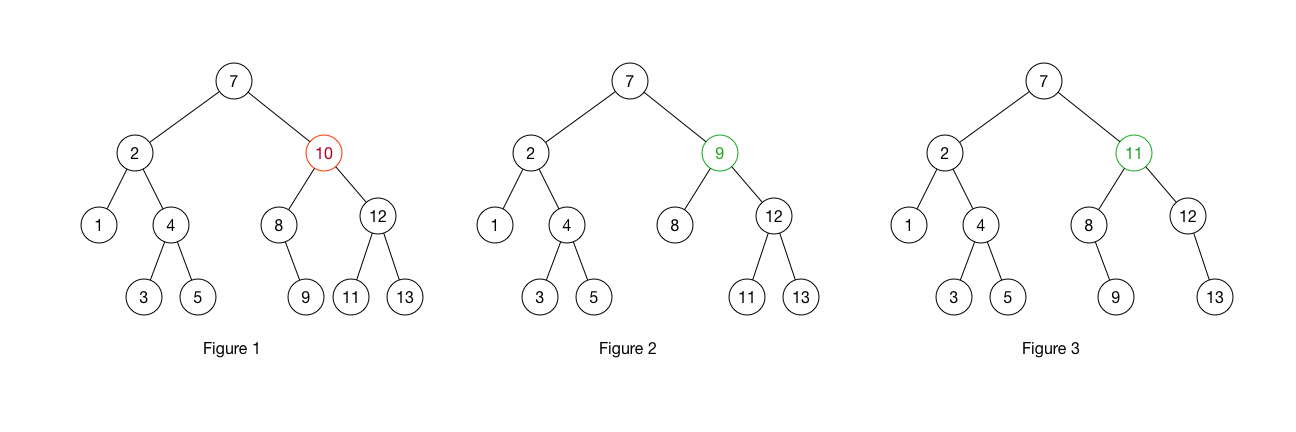
Deleting a node with two children

注意，只有被移除的节点有子节点时才需要替换填充。否则直接断开其与父节点的连接即可：

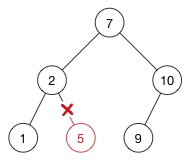
Deleting a leaf node

实现方案 1

理论差不多了，接下来我们看看怎么通过 Swift 实现一个二叉搜索树。有两种方案可以实现。首先，展示一个类（class）实现的版本，之后在展示如何通过枚举（enum）来实现。

下面是一个 BinarySearchTree 的类实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class BinarySearchTree<T: Comparable> {
  private(set) public var value: T
  private(set) public var parent: BinarySearchTree?
  private(set) public var left: BinarySearchTree?
  private(set) public var right: BinarySearchTree?

  public init(value: T) {
    self.value = value
  }

  public var isRoot: Bool {
    return parent == nil
  }

  public var isLeaf: Bool {
    return left == nil && right == nil
  }

  public var isLeftChild: Bool {
    return parent?.left === self
  }

  public var isRightChild: Bool {
    return parent?.right === self
  }

  public var hasLeftChild: Bool {
    return left != nil
  }

  public var hasRightChild: Bool {
    return right != nil
  }

  public var hasAnyChild: Bool {
    return hasLeftChild || hasRightChild
  }

  public var hasBothChildren: Bool {
    return hasLeftChild && hasRightChild
  }

  public var count: Int {
    return (left?.count ?? 0) + 1 + (right?.count ?? 0)
  }
}

该类仅描述了一个节点而不是整个树。类型是泛型，所以节点可以存储任何类型的数据。此外它还有对其 left 、right 以及 parent 节点的引用。

用法如下:

1
let tree = BinarySearchTree<Int>(value: 7)

count 属性用来统计某个节点的子树中拥有多少个节点。它不仅仅统计它的子节点，还统计它子节点的子子孙孙。如果该节点恰好是根节点，那么它统计的就是整个树的节点数。初始，count = 0。

注意： 由于 left, right, 和 parent 均是可选类型，所有可以充分利用 Swift 的可选链（?）和空合运算符（??）。当然也可以用 if let，但这样不够简洁。

批量插入

单个树节点自身是无意义的，可以通过下面的方法想树中插入新节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public func insert(value: T) {
  if value < self.value {
    if let left = left {
      left.insert(value: value)
    } else {
      left = BinarySearchTree(value: value)
      left?.parent = self
    }
  } else {
    if let right = right {
      right.insert(value: value)
    } else {
      right = BinarySearchTree(value: value)
      right?.parent = self
    }
  }
}

与其它树操作类似，插入是最容易通过递归实现的。通过与已有节点的比较，来确定是将它添加到左分支还是右分支。

如果没有左或右子节点，那么就创建一个 BinarySearchTree 对象作为新节点，然后通过设置 parent 属性，将它连接到树中。

注意： 由于二叉搜索树的关键就在与左小，右大，所以始终要从根开始执行插入，以保证在操作完毕后仍是一个有效的二叉搜索树！

构建一个完整的树:

1
2
3
4
5
6
let tree = BinarySearchTree<Int>(value: 7)
tree.insert(2)
tree.insert(5)
tree.insert(10)
tree.insert(9)
tree.insert(1)

注意： 为了之后的深入了解，插入的数应尽量随机。如果有序的插入，那么最终树的形可能就不对了。（译者：尽量保持树的平衡性）

为了方便操作，这里增加一个初始化方法，这样就可以通过 insert() 将数组中所有元素插入（到树中）了：

1
2
3
4
5
6
7
public convenience init(array: [T]) {
  precondition(array.count > 0)
  self.init(value: array.first!)
  for v in array.dropFirst() {
    insert(value: v)
  }
}

现在可以这样创建一棵树了:

1
let tree = BinarySearchTree<Int>(array: [7, 2, 5, 10, 9, 1])

数组中的首元素即为树的根。

Debug信息输出

处理复杂数据结构时，输出可读性强的 debug 信息大有助益。

1
2
3
4
5
6
7
8
9
10
11
12
13
extension BinarySearchTree: CustomStringConvertible {
  public var description: String {
    var s = ""
    if let left = left {
      s += "(\(left.description)) <- "
    }
    s += "\(value)"
    if let right = right {
      s += " -> (\(right.description))"
    }
    return s
  }
}

当调用 print(tree) 时, 会看到如下信息:

((1) <- 2 -> (5)) <- 7 -> ((9) <- 10)

根节点在中间。想象一下，是不是正好与下面的树相对应：

The tree

你可能会想如果插入相同的元素会如何呢？我们这里总是会将它插入右分支。尝试一下。

搜索

树中已经有值了，那么接下来我们做点什么呢？当然是查询！快速查询对象是二叉搜索树的一个主要应用。:-)

下面是 search() 的实现：

1
2
3
4
5
6
7
8
9
public func search(value: T) -> BinarySearchTree? {
  if value < self.value {
    return left?.search(value: value)
  } else if value > self.value {
    return right?.search(value: value)
  } else {
    return self  // found it!
  }
}

思路很简单：首先从当前节点开始（通常是根节点）进行比较。如果目标值小于当前节点的值，在左分支继续查询；如果大于，就在右分支继续。

如果已经没有节点可查了——即 left 或 right 为空——我们就返回 nil，表示查询的值在树中不存在。

注意： 在 Swift 中，使用可选链非常便捷；如果 left 为空， left?.search(value) 会自动返空。完全不需要通过 if 表示去判断。

搜索是一个递归过程，但你也可以通过简单循环来实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
public func search(_ value: T) -> BinarySearchTree? {
  var node: BinarySearchTree? = self
  while let n = node {
    if value < n.value {
      node = n.left
    } else if value > n.value {
      node = n.right
    } else {
      return node
    }
  }
  return nil
}

确保你已经理解这两种实现是等价的，依自己喜欢选用。但就我个人而言，相对于递归更倾向于迭代。;-)

下面是对搜索的测试:

1
2
3
4
tree.search(5)
tree.search(2)
tree.search(7)
tree.search(6)   // nil

前三行都会返回了相应的 BinaryTreeNode 对象。最后一行返回了 nil，因为没有节点包涵 6。

注意： 如果树中存在多个相同的对象，那么 search() 会返回 “最高的” 那个节点。之所以如此，是因为我们总是从根开始向下查找。

遍历

还记得遍历树中所有节点的 3 种方法吗？如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public func traverseInOrder(process: (T) -> Void) {
  left?.traverseInOrder(process: process)
  process(value)
  right?.traverseInOrder(process: process)
}

public func traversePreOrder(process: (T) -> Void) {
  process(value)
  left?.traversePreOrder(process: process)
  right?.traversePreOrder(process: process)
}

public func traversePostOrder(process: (T) -> Void) {
  left?.traversePostOrder(process: process)
  right?.traversePostOrder(process: process)
  process(value)
}

都能遍历，只是顺序不同。注意全部都是递归的。当没有左右子节点时，Swift 的可选链使对 traverseInOrder() 等的调用非常简洁明了。

按从小到大的顺序打印树中所有值：

1
tree.traverseInOrder { value in print(value) }

打印结果如下:

1
2
5
7
9
10

你还可以给树添加 map() 和 filter() 方法。 例如，下面是一个 map 方法的实现：

1
2
3
4
5
6
7
8

public func map(formula: (T) -> T) -> [T] {
  var a = [T]()
  if let left = left { a += left.map(formula: formula) }
  a.append(formula(value))
  if let right = right { a += right.map(formula: formula) }
  return a
}

map() 方法通过对树进行中序遍历，将 formula 闭包应用到树中的每个节点上，并将结果存放于一个数组中进行返回。

一个非常简单的 map() 应用例子：

1
2
3
public func toArray() -> [T] {
  return map { $0 }
}

它将树中内容反转成一个有序的数组。在 playground 中尝试一下：

1
tree.toArray()   // [1, 2, 5, 7, 9, 10]

作为练习，你自己可以尝试实现一个 filter 和 reduce。

批量移除

通过定义一些辅助方法，可以让代码（逻辑）更加清晰。

1
2
3
4
5
6
7
8
9
10
private func reconnectParentTo(node: BinarySearchTree?) {
  if let parent = parent {
    if isLeftChild {
      parent.left = node
    } else {
      parent.right = node
    }
  }
  node?.parent = parent
}

要修改一颗树需要修改大量的 parent 、 left 以及 right 引用。该方法正是为了解决这个问题。首先取得当前节点 self 的父节点，之后在把另一个节点连接为自己即 self 的子节点。

此外是需要一个方法用来返回最小和最大的节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public func minimum() -> BinarySearchTree {
  var node = self
  while let next = node.left {
    node = next
  }
  return node
}

public func maximum() -> BinarySearchTree {
  var node = self
  while let next = node.right {
    node = next
  }
  return node
}

余下的代码可读性很强，不在过多说明:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
@discardableResult public func remove() -> BinarySearchTree? {
  let replacement: BinarySearchTree?

  // Replacement for current node can be either biggest one on the left or
  // smallest one on the right, whichever is not nil
  if let right = right {
    replacement = right.minimum()
  } else if let left = left {
    replacement = left.maximum()
  } else {
    replacement = nil
  }

  replacement?.remove()

  // Place the replacement on current node's position
  replacement?.right = right
  replacement?.left = left
  right?.parent = replacement
  left?.parent = replacement
  reconnectParentTo(node:replacement)

  // The current node is no longer part of the tree, so clean it up.
  parent = nil
  left = nil
  right = nil

  return replacement
}

深度和高度

回想下节点的高度，即到其最底端叶子节点到距离。可以通过下面的方法计算得到：

1
2
3
4
5
6
7
public func height() -> Int {
  if isLeaf {
    return 0
  } else {
    return 1 + max(left?.height() ?? 0, right?.height() ?? 0)
  }
}

查询左右分支的高度，返回最高的那个。同样是一个递归过程。由于需要遍历该节点的所有的子节点，所以时间杂度是 **O(n)**。

注意： 这里使用 Swift 的空合运算符来处理 left 或 right 为空的情况。虽然用 if let 也不错，但是这样相对更简洁。

尝试一下:

1
tree.height()  // 2

还可以计算节点的 深度（depth），即与根节点的距离。代码如下：

1
2
3
4
5
6
7
8
9
public func depth() -> Int {
  var node = self
  var edges = 0
  while let parent = node.parent {
    node = parent
    edges += 1
  }
  return edges
}

通过 parent 应用向上（统计），直至根节点（它的 parent 为空）。这一操作的时间杂度是 **O(h)**。例如如下：

1
2
3
if let node9 = tree.search(9) {
  node9.depth()   // returns 2
}

前驱和后继（Predecessor and successor）

虽然二叉搜索树总是“有序的”，但这并不意味着顺序相连的数值在树中的位置也是相邻。

Example

注意，在查看左子节点之前，是没办法得到刚好小于 7 的那个数值的。它的左子节点是 2, 而不是刚好小于它的 5。

predecessor() 会返回那个在整个序列中正在位于当前值之前的那个节点：

1
2
3
4
5
6
7
8
9
10
11
12
public func predecessor() -> BinarySearchTree<T>? {
  if let left = left {
    return left.maximum()
  } else {
    var node = self
    while let parent = node.parent {
      if parent.value < value { return parent }
      node = parent
    }
    return nil
  }
}

如果有左子树，那就简单。此时左子树的最大值就是（该节点的）前驱。通过前面的图例可以得知这一点， 5 恰好是 7 的左分支上的做大值。

如果没有左子树，那就必须查找父节点，直到找到那个最小值。例如查找节点 9的前驱，持续向上查找，直至那个最先具有较小值的父节点，7。

successor() 与之相似，只不过是镜像相反的：

1
2
3
4
5
6
7
8
9
10
11
12
public func successor() -> BinarySearchTree<T>? {
  if let right = right {
    return right.minimum()
  } else {
    var node = self
    while let parent = node.parent {
      if parent.value > value { return parent }
      node = parent
    }
    return nil
  }
}

这两个方法的时间杂度都是 **O(h)**。

Note: There is a variation called a “threaded” binary tree where “unused” left and right pointers are repurposed to make direct links between predecessor and successor nodes. Very clever!（译者：待复习完线索二叉树之后在翻译此段内容）

二叉搜索树的有效性

要破坏二叉搜索树，可以通过对一个非根节点调用 insert() 以使其变为一个无效树。示例如下：

1
2
3
if let node1 = tree.search(1) {
  node1.insert(100)
}

根节点是 7，所以 100 必须被插入到树的右分支上。然而你却没有从根节点开始，反而是从树的左分支上的叶子开始插入。因此，100 被插入到了错误的位置！

进而导致 tree.search(100) 返回空值。

可以通过下的方法来检查一个树是不是一个有效的二叉搜索树：

1
2
3
4
5
6
public func isBST(minValue minValue: T, maxValue: T) -> Bool {
  if value < minValue || value > maxValue { return false }
  let leftBST = left?.isBST(minValue: minValue, maxValue: value) ?? true
  let rightBST = right?.isBST(minValue: value, maxValue: maxValue) ?? true
  return leftBST && rightBST
}

检查左分支的值是否小于当前节点的值，并且右分支的值大于当前值。

调用方法如下:

1
2
3
4
5
6
if let node1 = tree.search(1) {
  tree.isBST(minValue: Int.min, maxValue: Int.max)  // true
  node1.insert(100)                                 // EVIL!!!
  tree.search(100)                                  // nil
  tree.isBST(minValue: Int.min, maxValue: Int.max)  // false
}

实现方案 2

除了类可以实现二叉搜索树，枚举也是可以的。

区别就在于引用语义与值语义。基于类实现的树，一旦类被修改，那么内存中的相同实例都会被修改，而基于枚举的树是不可变的 —— 任何插入或删除都会给你一个基于原树的全新拷贝。至于那种方式更好，则完全取决于你的应用场景。

下面是一个枚举实现的二叉搜索树：

1
2
3
4
5
public enum BinarySearchTree<T: Comparable> {
  case Empty
  case Leaf(T)
  indirect case Node(BinarySearchTree, T, BinarySearchTree)
}

该枚举有三个 cases：

  • Empty 表示分支末端 (基于类实现的版本中用 nil 引用表示).
  • Leaf 表示没有子节点的叶子节点。
  • Node 表示拥有一个或两个子节点的节点。此处用 indirect 修饰，以便其可以持有 BinarySearchTree 类型的值，否则不是递归枚举。

注意： 这样的二叉树是没有指向父节点的引用的。这不是什么大问题，只是某些操作实现起来更麻烦一些。

这里通过递归实现，并且枚举的每种 case 都必须区别对待。例如，下面展示了如果统计节点数以及数的高度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public var count: Int {
  switch self {
  case .Empty: return 0
  case .Leaf: return 1
  case let .Node(left, _, right): return left.count + 1 + right.count
  }
}

public var height: Int {
  switch self {
  case .Empty: return -1
  case .Leaf: return 0
  case let .Node(left, _, right): return 1 + max(left.height, right.height)
  }
}

插入新节点:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public func insert(newValue: T) -> BinarySearchTree {
  switch self {
  case .Empty:
    return .Leaf(newValue)

  case .Leaf(let value):
    if newValue < value {
      return .Node(.Leaf(newValue), value, .Empty)
    } else {
      return .Node(.Empty, value, .Leaf(newValue))
    }

  case .Node(let left, let value, let right):
    if newValue < value {
      return .Node(left.insert(newValue), value, right)
    } else {
      return .Node(left, value, right.insert(newValue))
    }
  }
}

在 playground 中尝试一下:

1
2
3
4
5
6
var tree = BinarySearchTree.Leaf(7)
tree = tree.insert(2)
tree = tree.insert(5)
tree = tree.insert(10)
tree = tree.insert(9)
tree = tree.insert(1)

注意，每次的插入操作都会得到一个新的树对象，所以需要将结果重新赋给 tree 变量。

下面是搜索方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public func search(x: T) -> BinarySearchTree? {
  switch self {
  case .Empty:
    return nil
  case .Leaf(let y):
    return (x == y) ? self : nil
  case let .Node(left, y, right):
    if x < y {
      return left.search(x)
    } else if y < x {
      return right.search(x)
    } else {
      return self
    }
  }
}

大多数的方法都有相同的结构。

在 playground 中尝试一下:

1
2
3
tree.search(10)
tree.search(1)
tree.search(11)   // nil

要 debug 打印整个树，可以使用下面的方法：

1
2
3
4
5
6
7
8
9
10
extension BinarySearchTree: CustomDebugStringConvertible {
  public var debugDescription: String {
    switch self {
    case .Empty: return "."
    case .Leaf(let value): return "\(value)"
    case .Node(let left, let value, let right):
      return "(\(left.debugDescription) <- \(value) -> \(right.debugDescription))"
    }
  }
}

执行 print(tree) 的结果如下:

((1 <- 2 -> 5) <- 7 -> (9 <- 10 -> .))

中间是根节点，点表示已经没有子节点。

当树变的不在平衡

当二叉树的左右子树拥有相同数量的节点时，那么它是 平衡的（balanced）。此时树的高度是 log(n)，n 表示节点数。这是理想状态。

一旦一个分支显著的比另一个更长，搜索就会变的非常慢。不必要的检索大大增加。最坏的情况是，树的高度变为 n。此时树相对于二叉搜索树来说更像是一个链表（linked list），时间杂度也将退化到 **O(n)**。

保持二叉搜索树平衡性的一个方法就是以完全随机的顺序插入新节点。总体上可以很好的保证树的平衡性，但这是没法保证的，也不实际。

另一个办法就是使用 自平衡（self-balancing) 二叉树。这种数据结构会在插入或删除节点后进行自适应，以保证树的平衡性。欲了解更多，请参见平衡树（AVL tree）和红黑树（red-black tree）

最后

该系列文章翻译自 Raywenderlich 的开源项目：swift-algorithm-club，意在帮助有一定基础的同学进行回顾，如果你才接触，那么建议移步阅读详细教程

参见

Binary Search Tree on Wikipedia

由 Nicolas Ameghino 和 Matthijs Hollemans 联合发表于 Swift 算法社区

由 William Han 翻译